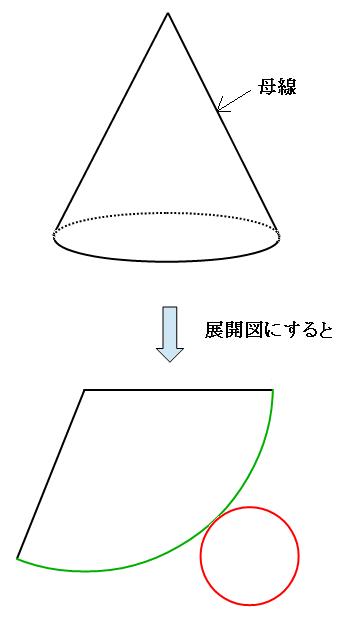
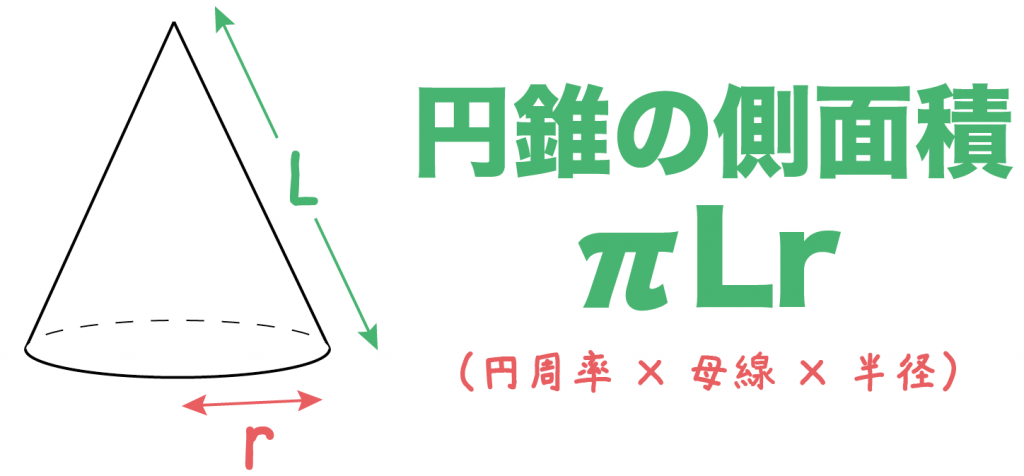
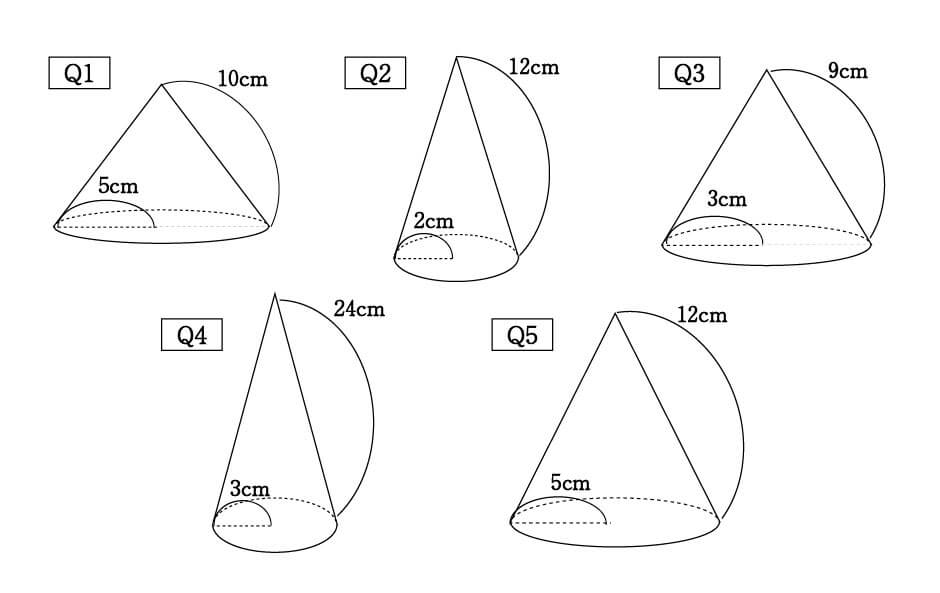
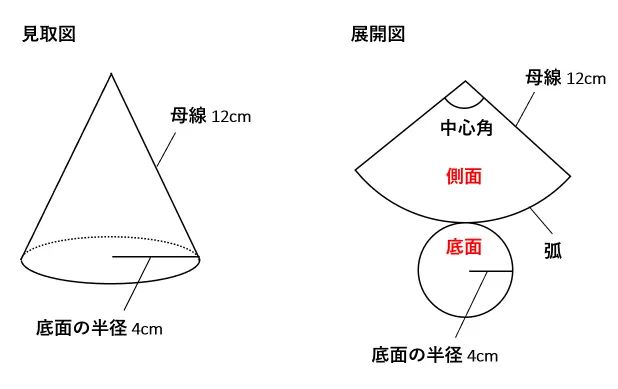
ですが、次の方法で簡単に計算することができます。 円すいの側面積 = 母線 × 半径 × π 5 × 3 × π = 15 π c m 2 問題表面積を求めなさい。 表面積 = 側面積 底面積 底面積は 9 π c m 2 、側面積は 15 π c m 2 よって、表面積は 15 π 9 π = 24 π c m 2
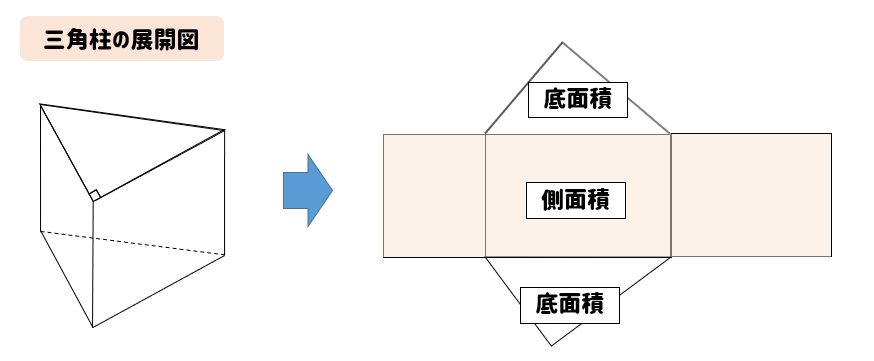
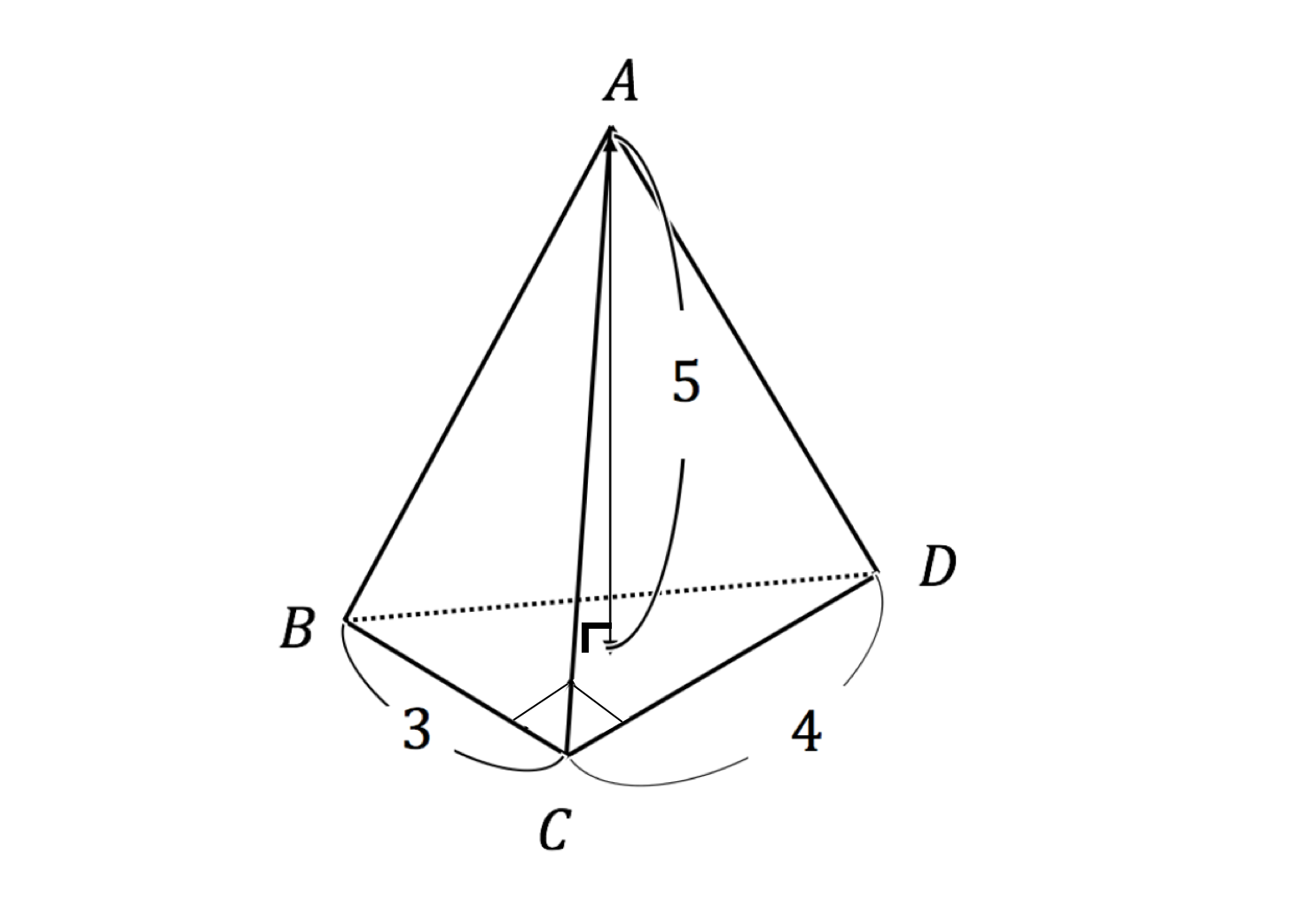
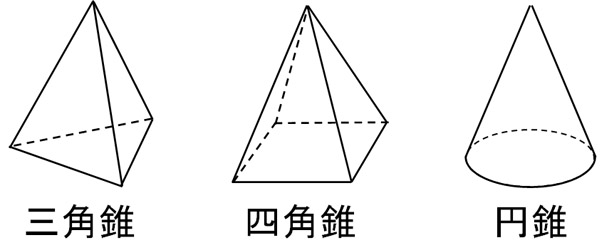
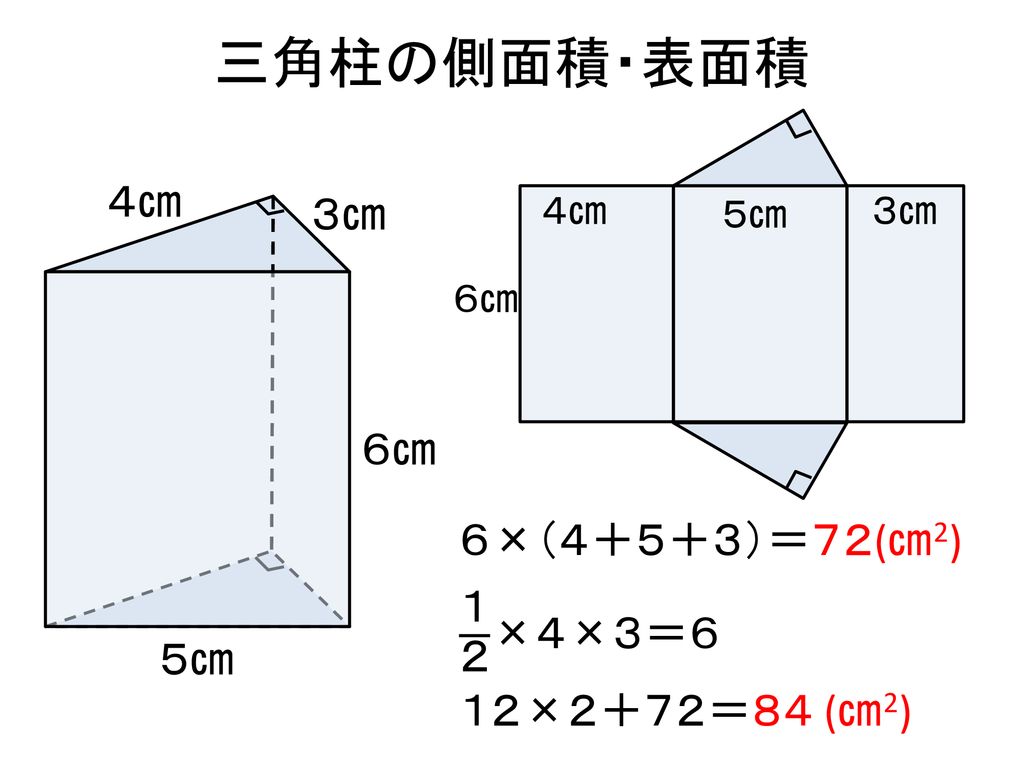
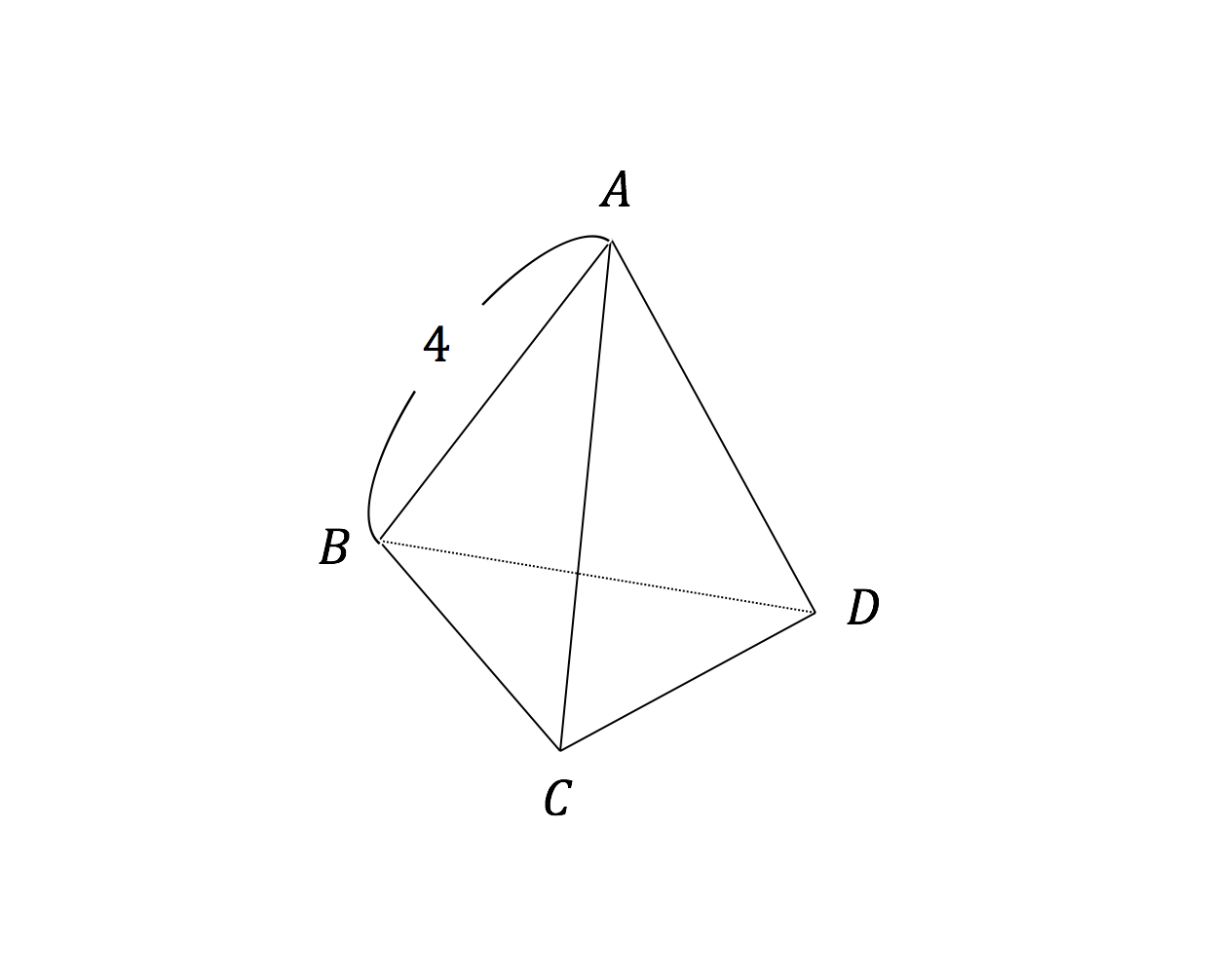
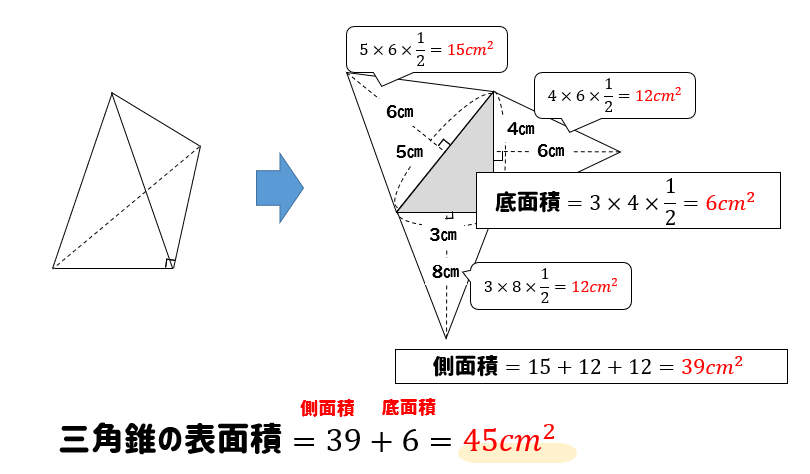
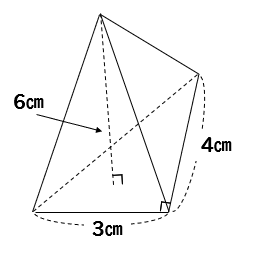
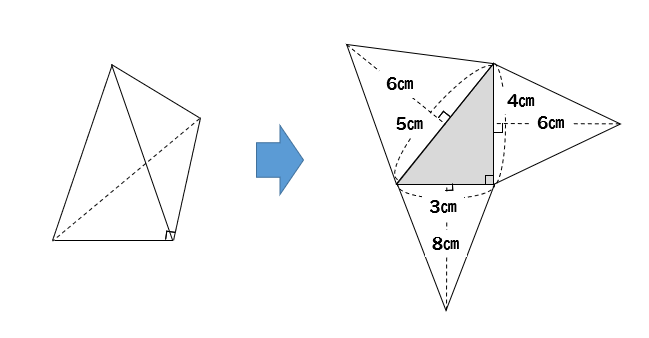
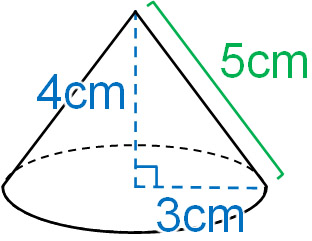
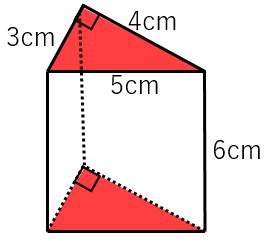
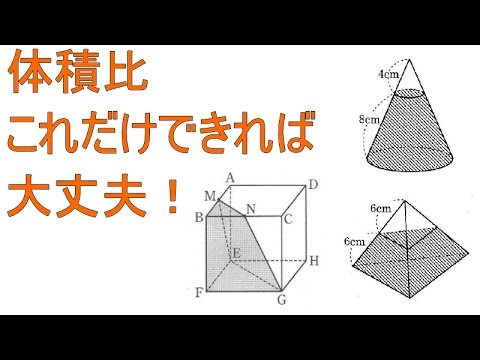
三角錐 表面積 求め方-三角錐の表面積=底面積 側面積(三角形 つ分) では、実際に問題を解いてみましょう。 次の三角錐の表面積を求めなさい。 ※長さはテキトーに決めましたので、図形的にあり得ない大きさになっているかもしれません (^^;)あくまで計算方法を紹介するための例題です。 展開図のイメージがつくれたら、あとはそれぞれを計算するだけです。 〇 三角錐の表面積は底面と側面(三角形3つ分)をあわ次の図形の体積と表面積を求めよ。 (1)底面が1辺6cmの正方形、側面はすべて合同で底辺が6cm、高さが5cmの三角形の四角錐。 また四角錐の高さは4cmとする。 (2)底面が半径5cm、母線が13cm、高さが12cmの円錐。 (1)『体積=底面積×高さ× 1 3 1 3 』なので、 6 ×6 ×4 × 1 3=48cm3 6 × 6 × 4 × 1 3 = 48 c m 3 側面積は底辺6cm、高さ5cmの三角形が4つの面積をあわせたものなので
三角錐 表面積 求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
 |  | |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「三角錐 表面積 求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |
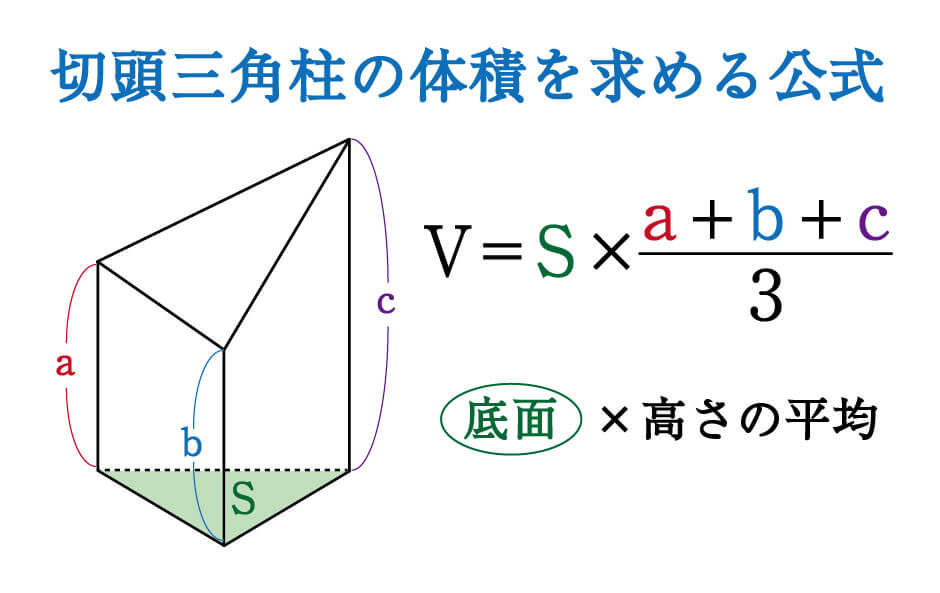
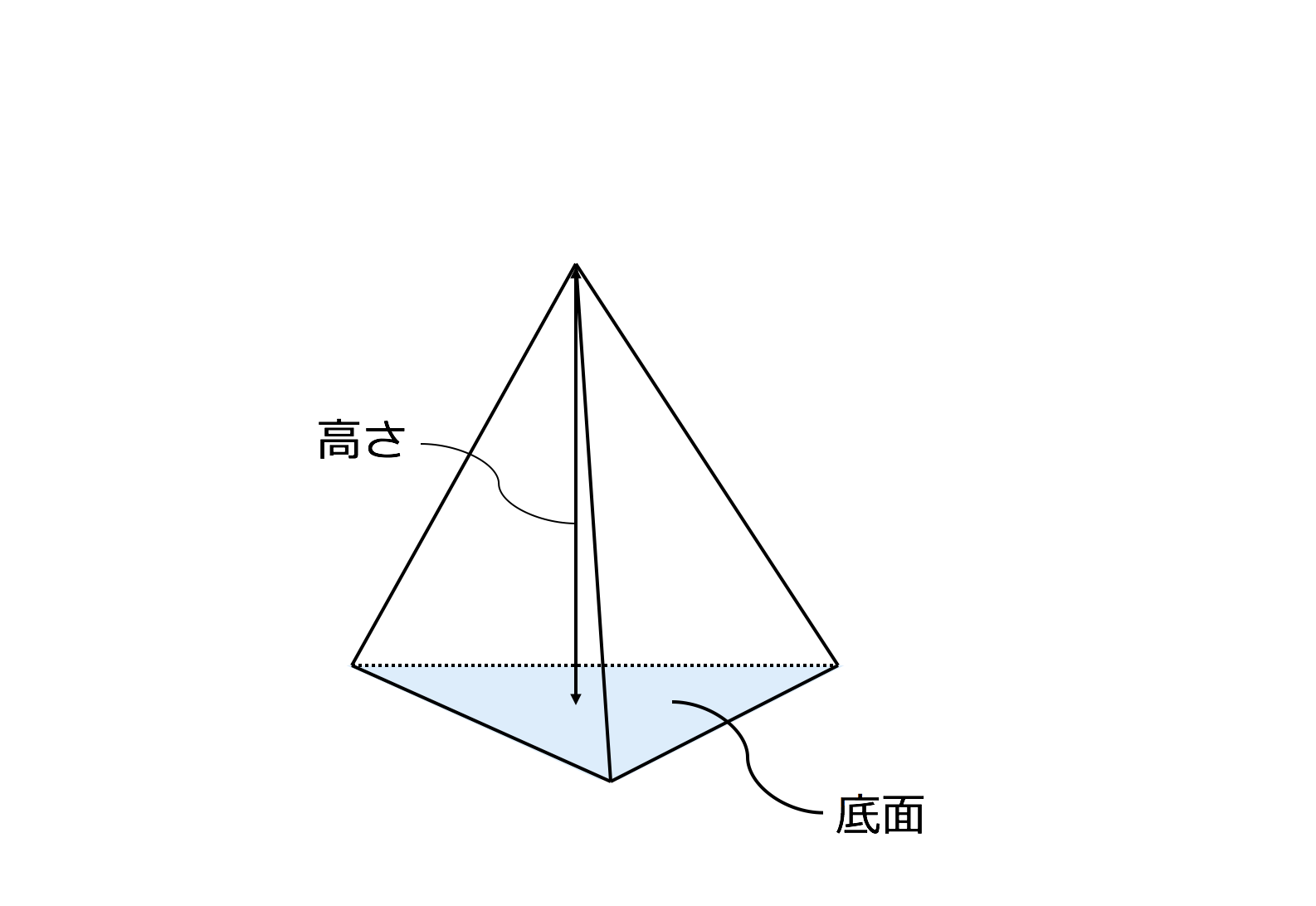
三角錐の体積の求め方の公式 まずは三角錐の体積を求める公式です。 こちらには非常に便利な公式が与えられています。 それは、 (三角錐の体積)= (底面積)× (高さ)× です。 三角柱であれば、 (三角錐の体積)= (底面積)× (高さ) で求めることができます。 一方で、図形のてっぺんがとんがっている三角錐の体積を求める場合、必ず をします。 なぜ をしなければならないのかについては、少 円錐の半径をr、母線の長さをLとすると、円錐の表面積はつぎのように計算できちゃうんだ。 πr(L+r) つまり、 (円周率)×(半径)×(母線+半径) ってことだね。 見ての通り、ちょー便利な計算公式なんだけど、 忘れたらヤバい っていうリスクがあるんだ。 だから、 公式に頼らない円錐の表面積の求め方 をおぼえておくと便利だよ。 円錐の表面積の求め方がわかる3ステッ
Incoming Term: 三角錐 表面積 求め方,




0 件のコメント:
コメントを投稿